BREAKING NEWS
LATEST POSTS
-
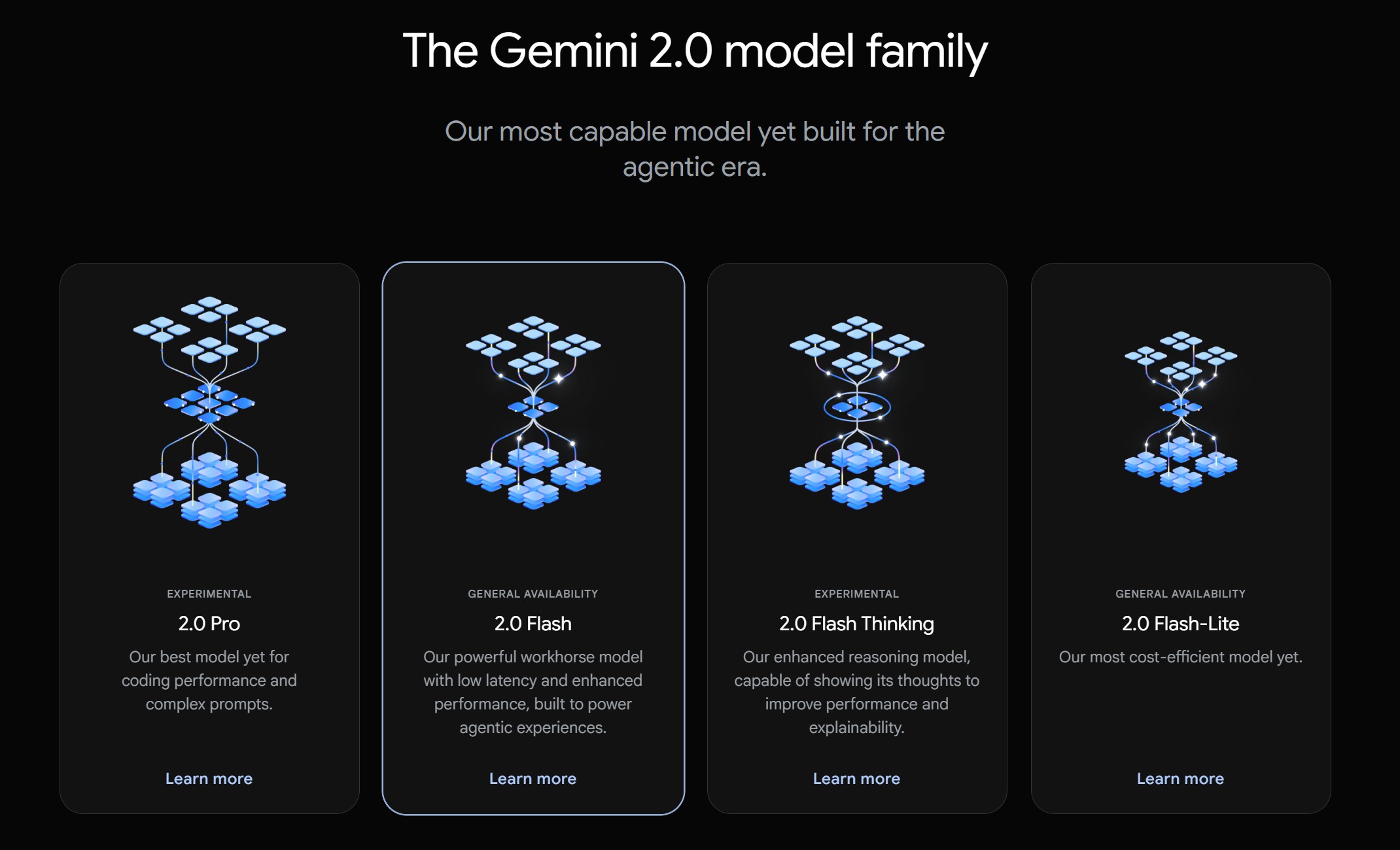
Google Gemini 2.0 Flash new AI model extremely proficient at removing watermarks from images
-
Stability.ai – Introducing Stable Virtual Camera: Multi-View Video Generation with 3D Camera Control
Capabilities
Stable Virtual Camera offers advanced capabilities for generating 3D videos, including:
- Dynamic Camera Control: Supports user-defined camera trajectories as well as multiple dynamic camera paths, including: 360°, Lemniscate (∞ shaped path), Spiral, Dolly Zoom In, Dolly Zoom Out, Zoom In, Zoom Out, Move Forward, Move Backward, Pan Up, Pan Down, Pan Left, Pan Right, and Roll.
- Flexible Inputs: Generates 3D videos from just one input image or up to 32.
- Multiple Aspect Ratios: Capable of producing videos in square (1:1), portrait (9:16), landscape (16:9), and other custom aspect ratios without additional training.
- Long Video Generation: Ensures 3D consistency in videos up to 1,000 frames, enabling seamless
Model limitations
In its initial version, Stable Virtual Camera may produce lower-quality results in certain scenarios. Input images featuring humans, animals, or dynamic textures like water often lead to degraded outputs. Additionally, highly ambiguous scenes, complex camera paths that intersect objects or surfaces, and irregularly shaped objects can cause flickering artifacts, especially when target viewpoints differ significantly from the input images.

-
Sony tests AI-powered Playstation characters
https://www.independent.co.uk/tech/ai-playstation-characters-sony-ps5-chatgpt-b2712813.html
A demo video, first reported by The Verge, showed an AI version of the character Aloy from the Playstation game Horizon Forbidden West conversing through voice prompts during gameplay on the PS5 console.
The character’s facial expressions are also powered by Sony’s advanced AI software Mockingbird, while the speech artificially replicates the voice of the actor Ashly Burch.

-
BEAR – BE-A-Rigger – Maya Rigging Tool
https://github.com/Grackable/bear_core
BEAR claims to be the most intuitive and easy-to-use rigging tool available, offering production-proven features that streamline the rigging workflow for maximum efficiency and consistency.
FEATURED POSTS
-
ComfyDock – The Easiest (Free) Way to Safely Run ComfyUI Sessions in a Boxed Container
https://www.reddit.com/r/comfyui/comments/1j2x4qv/comfydock_the_easiest_free_way_to_run_comfyui_in/
ComfyDock is a tool that allows you to easily manage your ComfyUI environments via Docker.
Common Challenges with ComfyUI
- Custom Node Installation Issues: Installing new custom nodes can inadvertently change settings across the whole installation, potentially breaking the environment.
- Workflow Compatibility: Workflows are often tested with specific custom nodes and ComfyUI versions. Running these workflows on different setups can lead to errors and frustration.
- Security Risks: Installing custom nodes directly on your host machine increases the risk of malicious code execution.
How ComfyDock Helps
- Environment Duplication: Easily duplicate your current environment before installing custom nodes. If something breaks, revert to the original environment effortlessly.
- Deployment and Sharing: Workflow developers can commit their environments to a Docker image, which can be shared with others and run on cloud GPUs to ensure compatibility.
- Enhanced Security: Containers help to isolate the environment, reducing the risk of malicious code impacting your host machine.

-
sRGB vs REC709 – An introduction and FFmpeg implementations
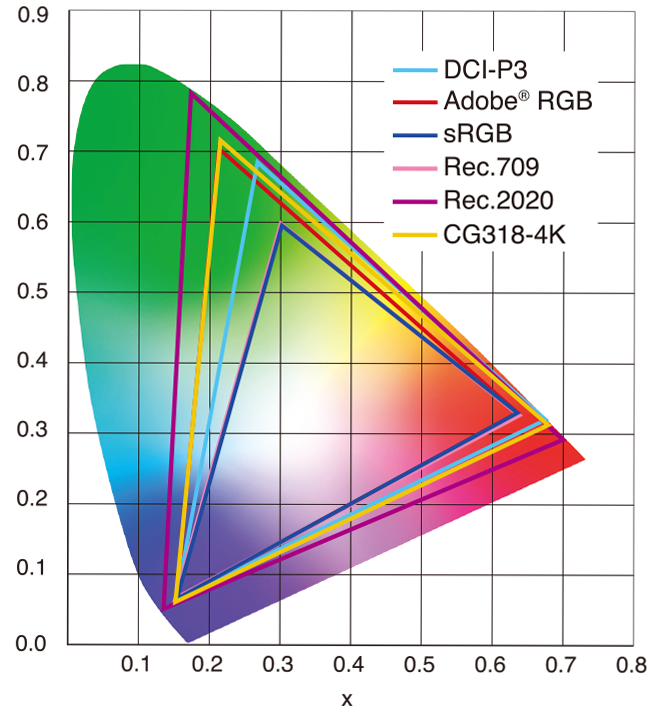
1. Basic Comparison
- What they are
- sRGB: A standard “web”/computer-display RGB color space defined by IEC 61966-2-1. It’s used for most monitors, cameras, printers, and the vast majority of images on the Internet.
- Rec. 709: An HD-video color space defined by ITU-R BT.709. It’s the go-to standard for HDTV broadcasts, Blu-ray discs, and professional video pipelines.
- Why they exist
- sRGB: Ensures consistent colors across different consumer devices (PCs, phones, webcams).
- Rec. 709: Ensures consistent colors across video production and playback chains (cameras → editing → broadcast → TV).
- What you’ll see
- On your desktop or phone, images tagged sRGB will look “right” without extra tweaking.
- On an HDTV or video-editing timeline, footage tagged Rec. 709 will display accurate contrast and hue on broadcast-grade monitors.
2. Digging Deeper
Feature sRGB Rec. 709 White point D65 (6504 K), same for both D65 (6504 K) Primaries (x,y) R: (0.640, 0.330) G: (0.300, 0.600) B: (0.150, 0.060) R: (0.640, 0.330) G: (0.300, 0.600) B: (0.150, 0.060) Gamut size Identical triangle on CIE 1931 chart Identical to sRGB Gamma / transfer Piecewise curve: approximate 2.2 with linear toe Pure power-law γ≈2.4 (often approximated as 2.2 in practice) Matrix coefficients N/A (pure RGB usage) Y = 0.2126 R + 0.7152 G + 0.0722 B (Rec. 709 matrix) Typical bit-depth 8-bit/channel (with 16-bit variants) 8-bit/channel (10-bit for professional video) Usage metadata Tagged as “sRGB” in image files (PNG, JPEG, etc.) Tagged as “bt709” in video containers (MP4, MOV) Color range Full-range RGB (0–255) Studio-range Y′CbCr (Y′ [16–235], Cb/Cr [16–240])
Why the Small Differences Matter
(more…) - What they are
-
What Is The Resolution and view coverage Of The human Eye. And what distance is TV at best?
https://www.discovery.com/science/mexapixels-in-human-eye
About 576 megapixels for the entire field of view.
Consider a view in front of you that is 90 degrees by 90 degrees, like looking through an open window at a scene. The number of pixels would be:
90 degrees * 60 arc-minutes/degree * 1/0.3 * 90 * 60 * 1/0.3 = 324,000,000 pixels (324 megapixels).At any one moment, you actually do not perceive that many pixels, but your eye moves around the scene to see all the detail you want. But the human eye really sees a larger field of view, close to 180 degrees. Let’s be conservative and use 120 degrees for the field of view. Then we would see:
120 * 120 * 60 * 60 / (0.3 * 0.3) = 576 megapixels.
Or.
7 megapixels for the 2 degree focus arc… + 1 megapixel for the rest.
https://clarkvision.com/articles/eye-resolution.html
Details in the post
-
Convert between light exposure and intensity
import math,sys def Exposure2Intensity(exposure): exp = float(exposure) result = math.pow(2,exp) print(result) Exposure2Intensity(0) def Intensity2Exposure(intensity): inarg = float(intensity) if inarg == 0: print("Exposure of zero intensity is undefined.") return if inarg < 1e-323: inarg = max(inarg, 1e-323) print("Exposure of negative intensities is undefined. Clamping to a very small value instead (1e-323)") result = math.log(inarg, 2) print(result) Intensity2Exposure(0.1)Why Exposure?
Exposure is a stop value that multiplies the intensity by 2 to the power of the stop. Increasing exposure by 1 results in double the amount of light.
Artists think in “stops.” Doubling or halving brightness is easy math and common in grading and look-dev.
Exposure counts doublings in whole stops:- +1 stop = ×2 brightness
- −1 stop = ×0.5 brightness
This gives perceptually even controls across both bright and dark values.
Why Intensity?
Intensity is linear.
It’s what render engines and compositors expect when:- Summing values
- Averaging pixels
- Multiplying or filtering pixel data
Use intensity when you need the actual math on pixel/light data.
Formulas (from your Python)
- Intensity from exposure: intensity = 2**exposure
- Exposure from intensity: exposure = log₂(intensity)
Guardrails:
- Intensity must be > 0 to compute exposure.
- If intensity = 0 → exposure is undefined.
- Clamp tiny values (e.g.
1e−323) before using log₂.
Use Exposure (stops) when…
- You want artist-friendly sliders (−5…+5 stops)
- Adjusting look-dev or grading in even stops
- Matching plates with quick ±1 stop tweaks
- Tweening brightness changes smoothly across ranges
Use Intensity (linear) when…
- Storing raw pixel/light values
- Multiplying textures or lights by a gain
- Performing sums, averages, and filters
- Feeding values to render engines expecting linear data
Examples
- +2 stops → 2**2 = 4.0 (×4)
- +1 stop → 2**1 = 2.0 (×2)
- 0 stop → 2**0 = 1.0 (×1)
- −1 stop → 2**(−1) = 0.5 (×0.5)
- −2 stops → 2**(−2) = 0.25 (×0.25)
- Intensity 0.1 → exposure = log₂(0.1) ≈ −3.32
Rule of thumb
Think in stops (exposure) for controls and matching.
Compute in linear (intensity) for rendering and math.