BREAKING NEWS
LATEST POSTS
-
Python – The Black code style formatting
https://black.readthedocs.io/en/stable/the_black_code_style/current_style.html
The Black code style guide emphasizes consistency, readability, and minimizing diffs in Python code. Key formatting rules include ignoring previous formatting, preferring double quotes, adding trailing commas, and wrapping lines to fit within 88 characters. Black standardizes whitespace usage, avoids unnecessary vertical space, and ensures uniform handling of parentheses, comments, and numeric literals. The formatter also aligns with PEP 8 and PEP 257 standards, and provides options to adjust line length and skip string normalization for specific projects.
-
Want to build a start up company that lasts? Think three-layer cake
https://www.fastcompany.com/91131427/want-to-build-a-company-that-lasts-think-three-layer-cake
Building a successful business requires a focus on three key elements: product excellence, go-to-market strategy, and operational excellence. Neglecting any of these areas can lead to failure, as evidenced by the high percentage of startups that don’t make it past the five-year mark. Founders and CEOs must ensure a solid product foundation while also integrating effective sales, marketing, and management strategies to achieve sustainable growth and scale.
- Foundation: Product Excellence, Core Values and Mission
- Core Values: These are the guiding principles that dictate behavior and action within the company. They form the ethical foundation and are crucial for maintaining consistency in decision-making.
- Mission: This defines the company’s purpose and goals. A clear and compelling mission helps align the team and provides a sense of direction.
- Efficiency and Scalability: This layer focuses on creating efficient processes that can scale as the company grows. Streamlined operations reduce costs and increase productivity.
- Structure: Operational Excellence and Innovation
- Operational Excellence: Efficient processes, quality control, and continuous improvement fall into this layer. Ensuring that the company operates smoothly and effectively is crucial for sustainability.
- Innovation: Staying competitive requires innovation. This involves developing new products, services, or processes that add value and keep the company relevant in the market.
- Quality Control and Continuous Improvement: Ensuring that operational processes are of high quality and constantly improving helps maintain product excellence and customer satisfaction.
- Technology and Infrastructure: Investing in the right technology and infrastructure to support business operations is vital. This includes everything from manufacturing equipment to software systems that enhance operational efficiency.
- Strategy: Go-to-Market Strategy, Vision and Long-Term Planning
- Vision: A forward-looking vision inspires and motivates the team. It outlines where the company aims to be in the future and helps in setting long-term goals.
- Strategic Planning: This involves setting long-term goals and determining the actions and resources needed to achieve them. It includes market analysis, competitive strategy, and growth planning.
- Market Understanding: A deep understanding of the target market, including customer segments, competitors, and market trends, is essential. This knowledge helps in positioning the product effectively.
- Marketing and Sales Execution: This involves creating a robust marketing plan that includes branding, messaging, and advertising strategies to attract and retain customers. Additionally, building a strong sales strategy ensures that the product reaches the right customers through the right channels.
- Customer Acquisition and Retention: Effective strategies for acquiring new customers and retaining existing ones are critical. This includes loyalty programs, customer service excellence, and engagement initiatives.
- Foundation: Product Excellence, Core Values and Mission
-
Raspberry Pi is getting in on AI
https://www.theverge.com/2024/6/4/24170818/raspberry-pi-ai-chip-hailo-devices
As the AI craze continues, even the microcomputer company Raspberry Pi plans to sell an AI chip. It’s integrated with Raspberry Pi’s camera software and can run AI-based applications like chatbots natively on the tiny computer.
-
BorisFX Silhouette 2024 – What’s New in Roto
https://cdn.borisfx.com/borisfx/store/silhouette/2024-0/Silhouette-2024-WhatsNew.pdf
Matte Assist ML
Automatically generates a matte over time based on single or multiple
keyframed roto shapes or input mattes using machine learning object
segmentation and propagation.Optical Flow ML
Generates machine learning powered optical flow data for use in one of the
Roto based node’s Flow Tracker: Roto, Roto Blend, Tracker, Power Mask,
Morph and Depth. Optical flow estimates per-pixel motion between frames and
can be used to track shapes and objects.Retime ML
A machine learning motion estimation and retiming model that produces
smooth motion. Expands or contracts the timing of a selected range of frames. -
Eating rocks and other shocking Google AI answers we’ve seen so far
https://www.fastcompany.com/91132974/shocking-google-ai-overview-answers
No. Do NOT eat rocks or put them into food!
-
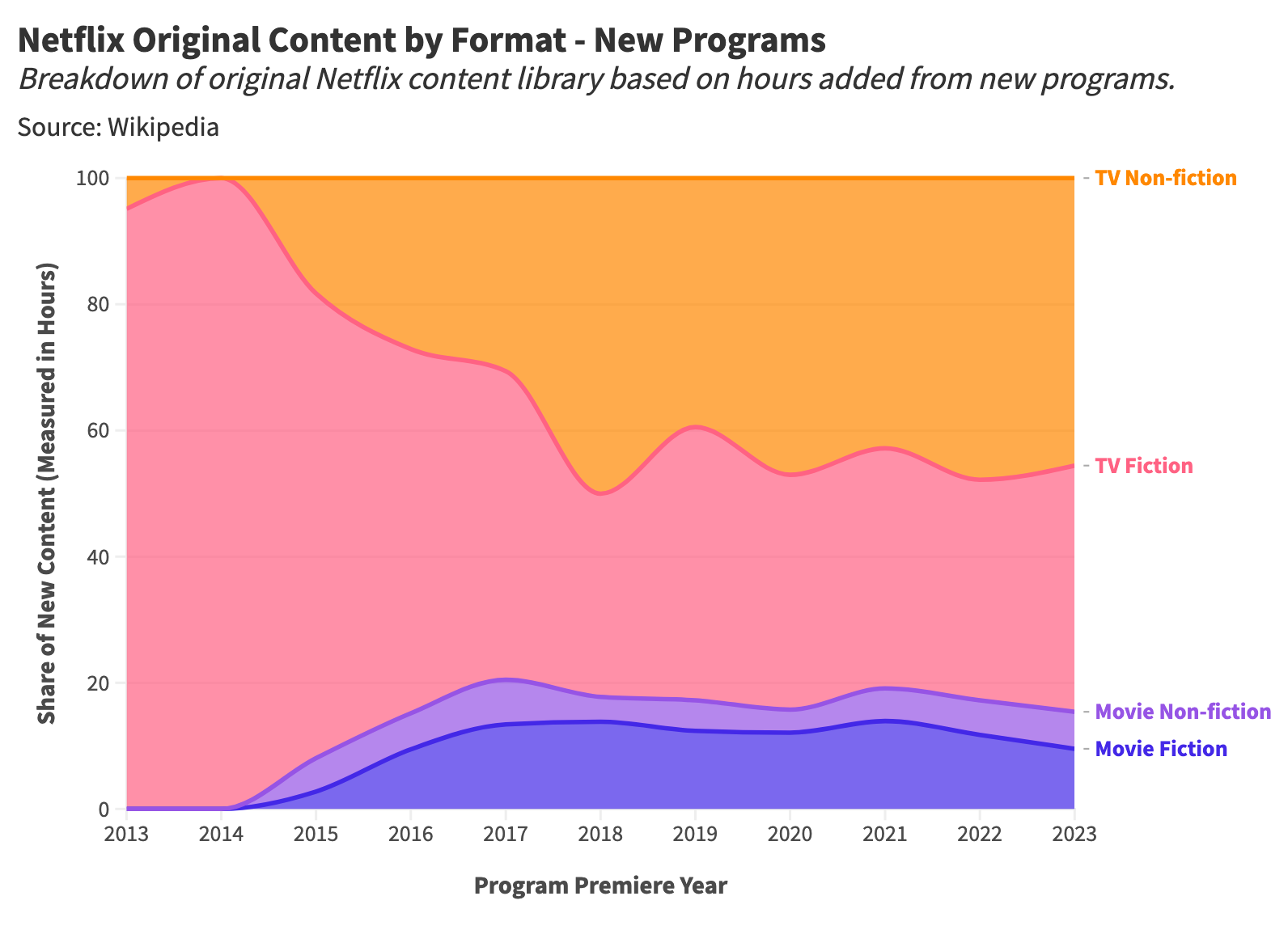
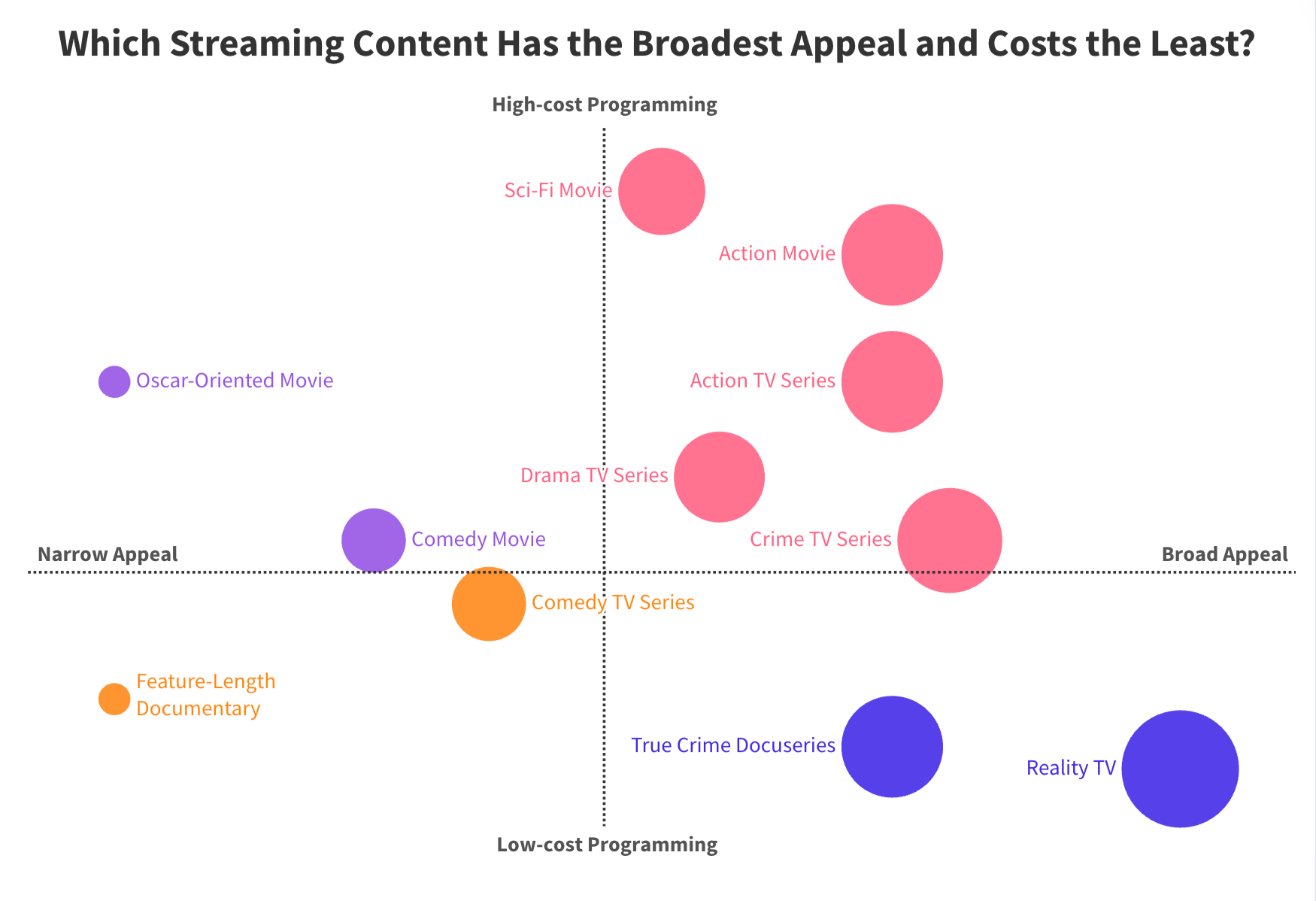
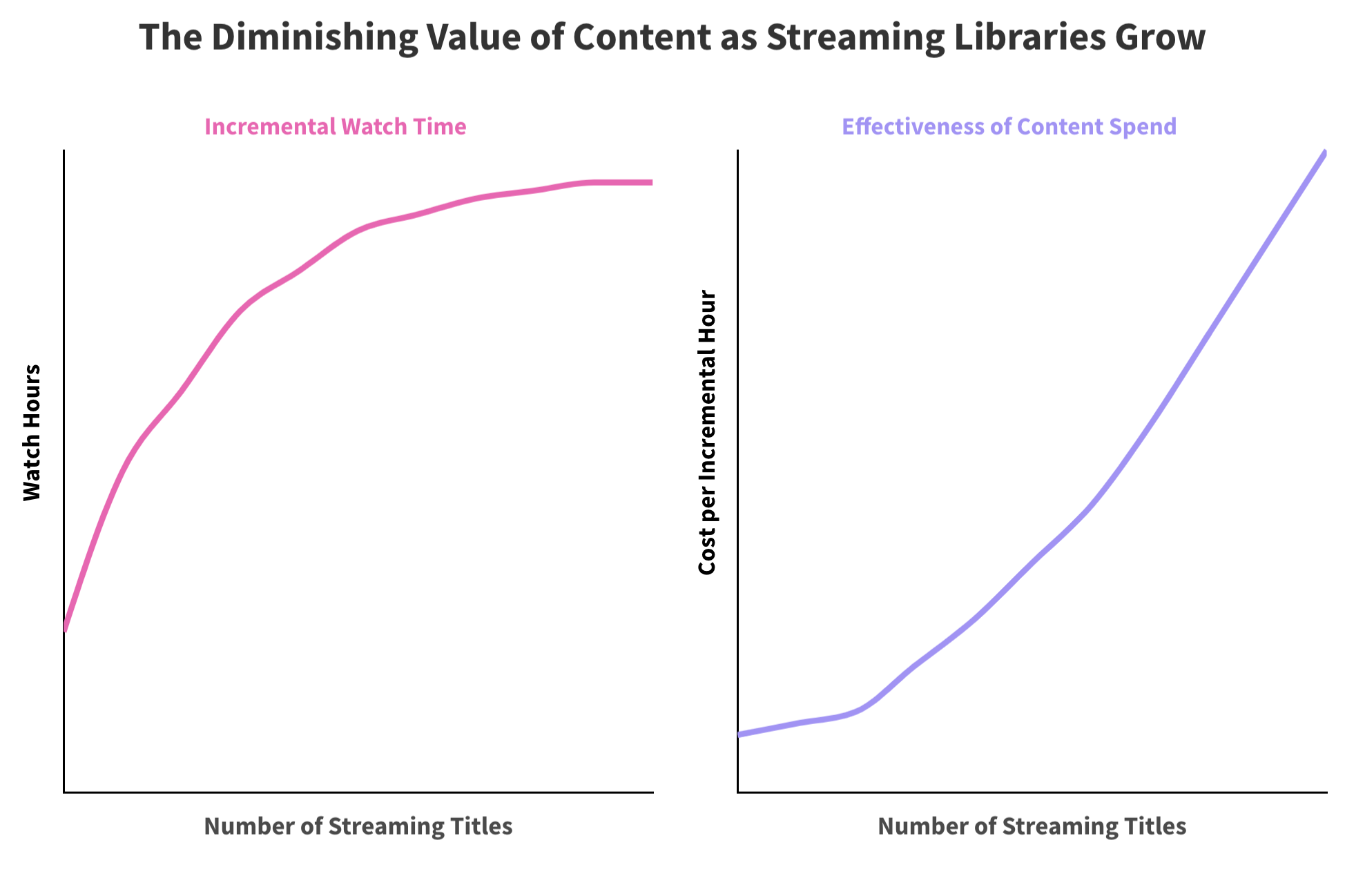
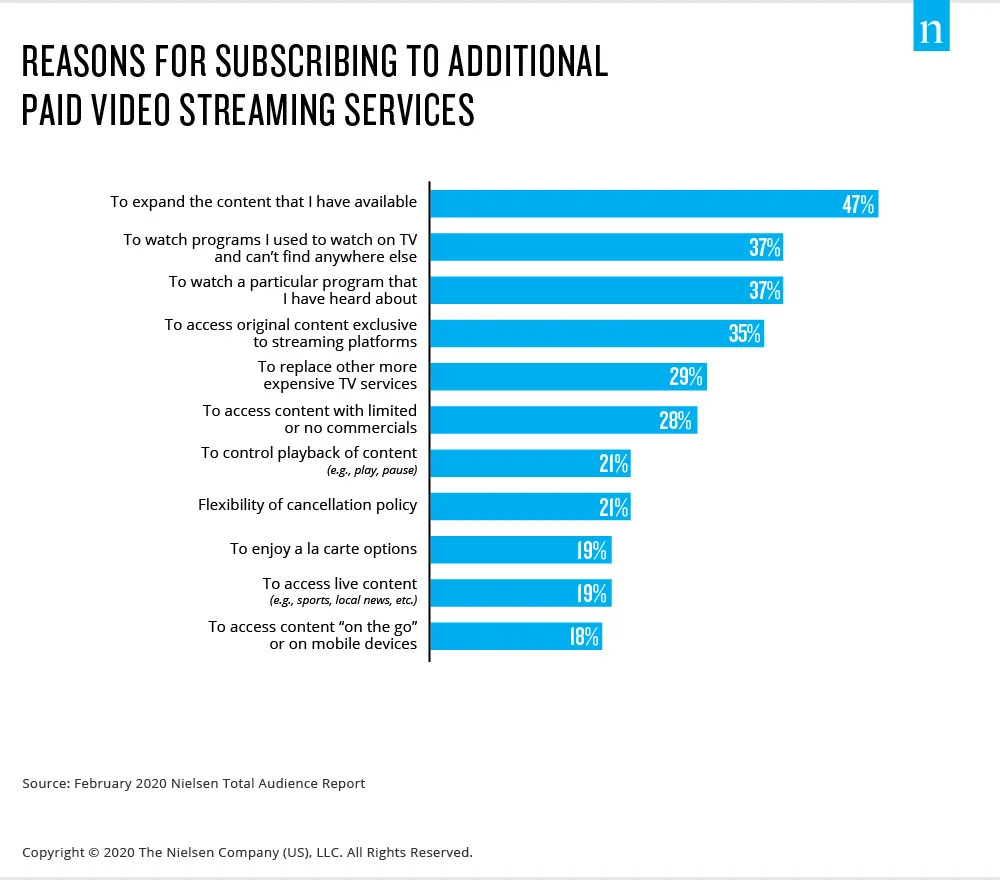
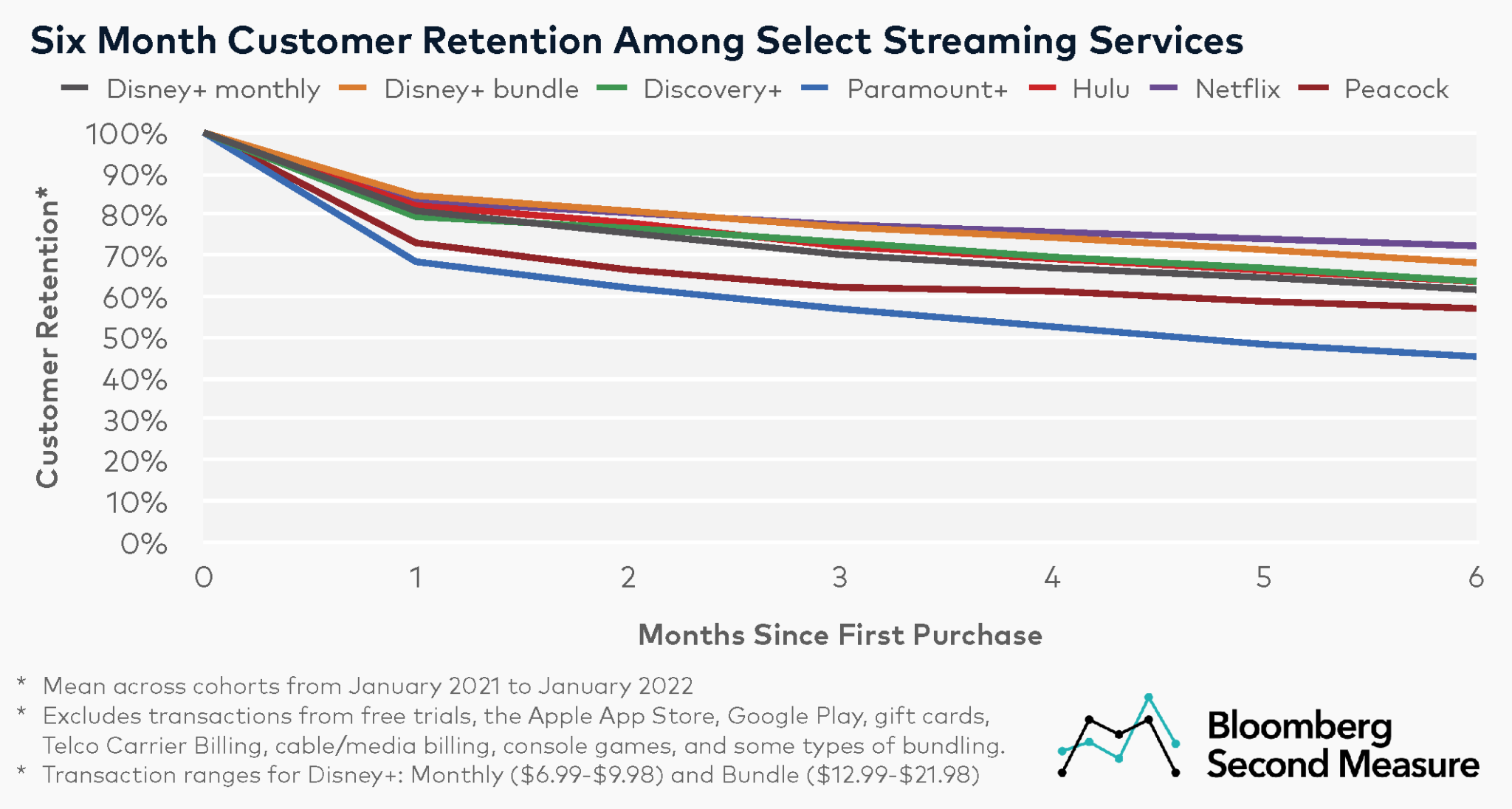
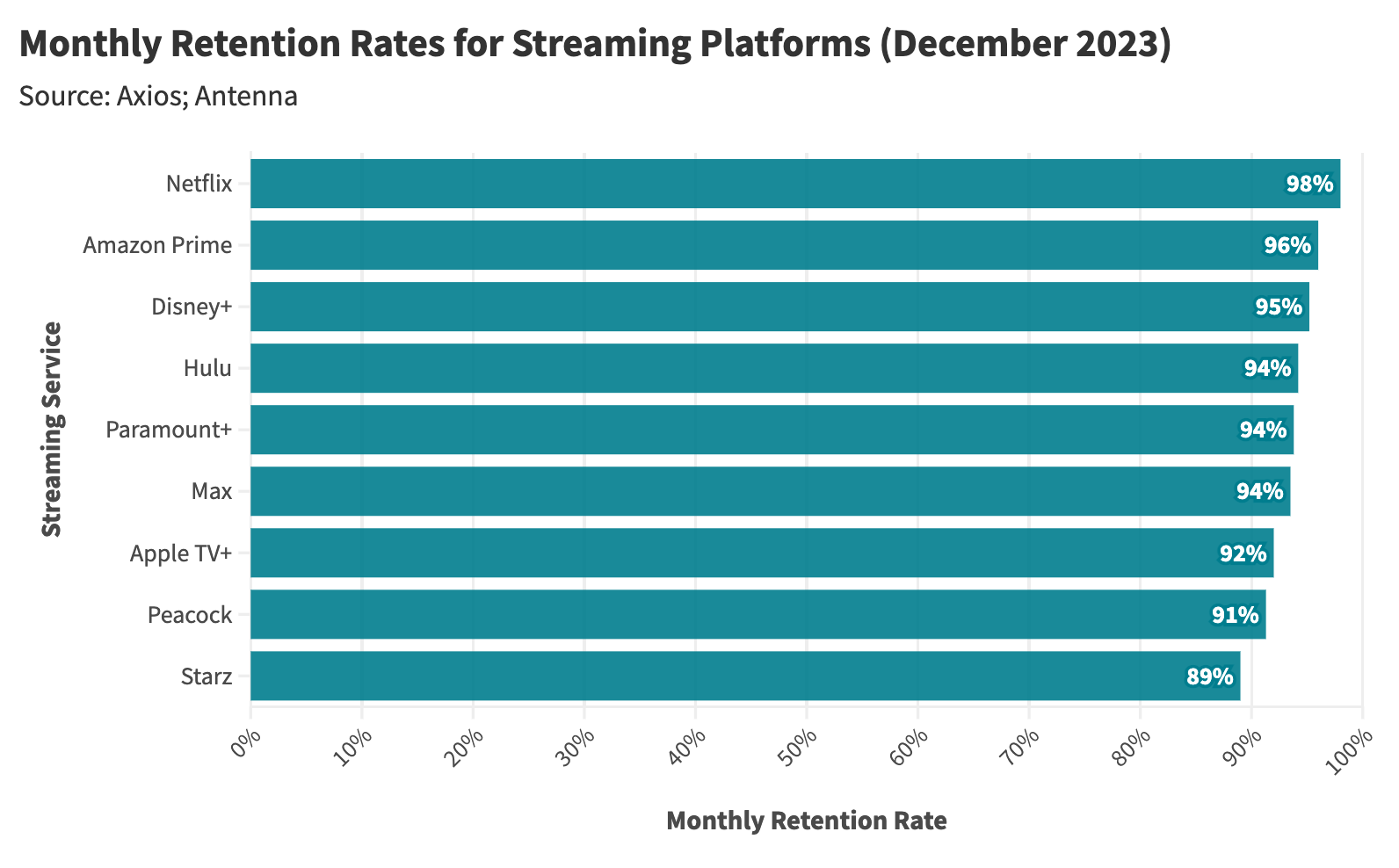
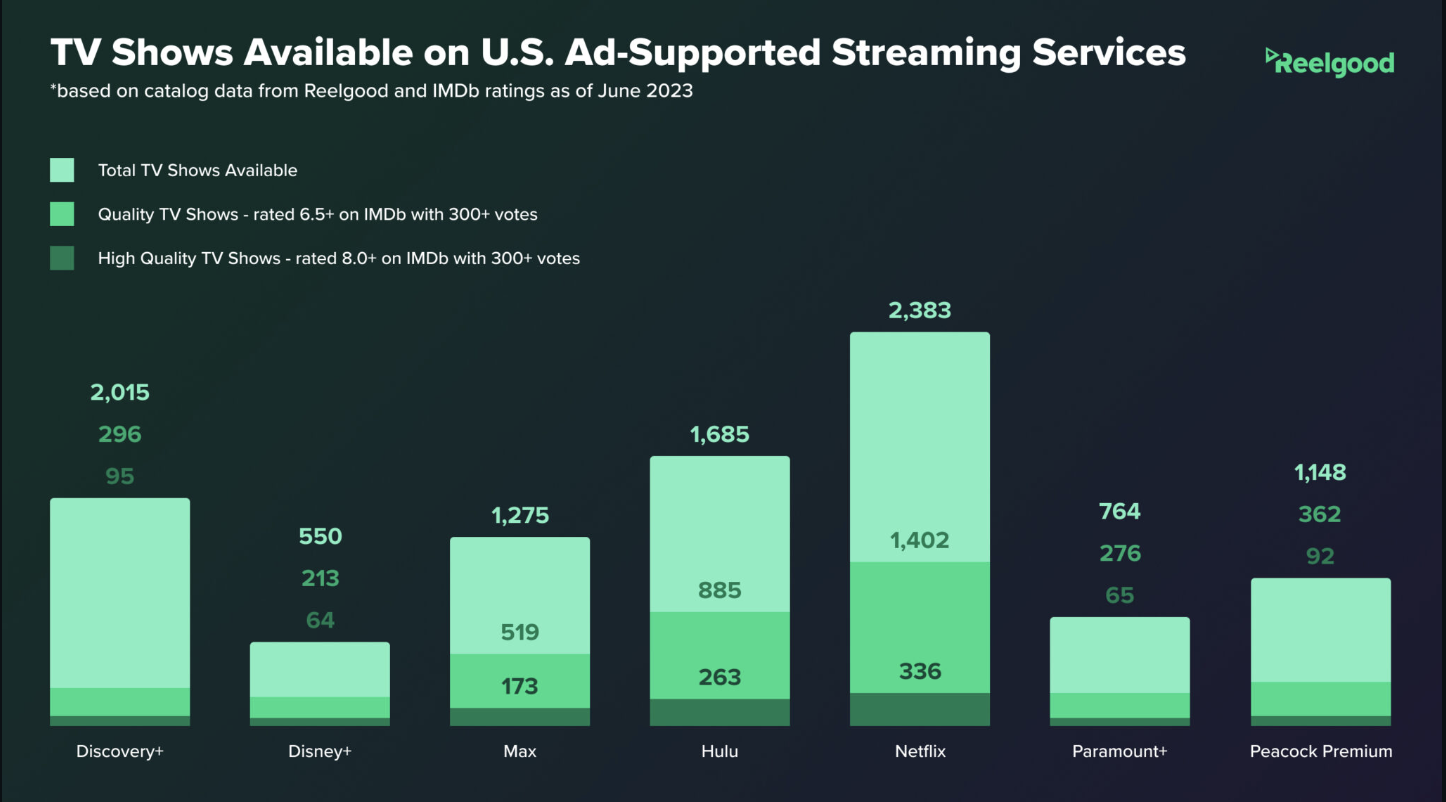
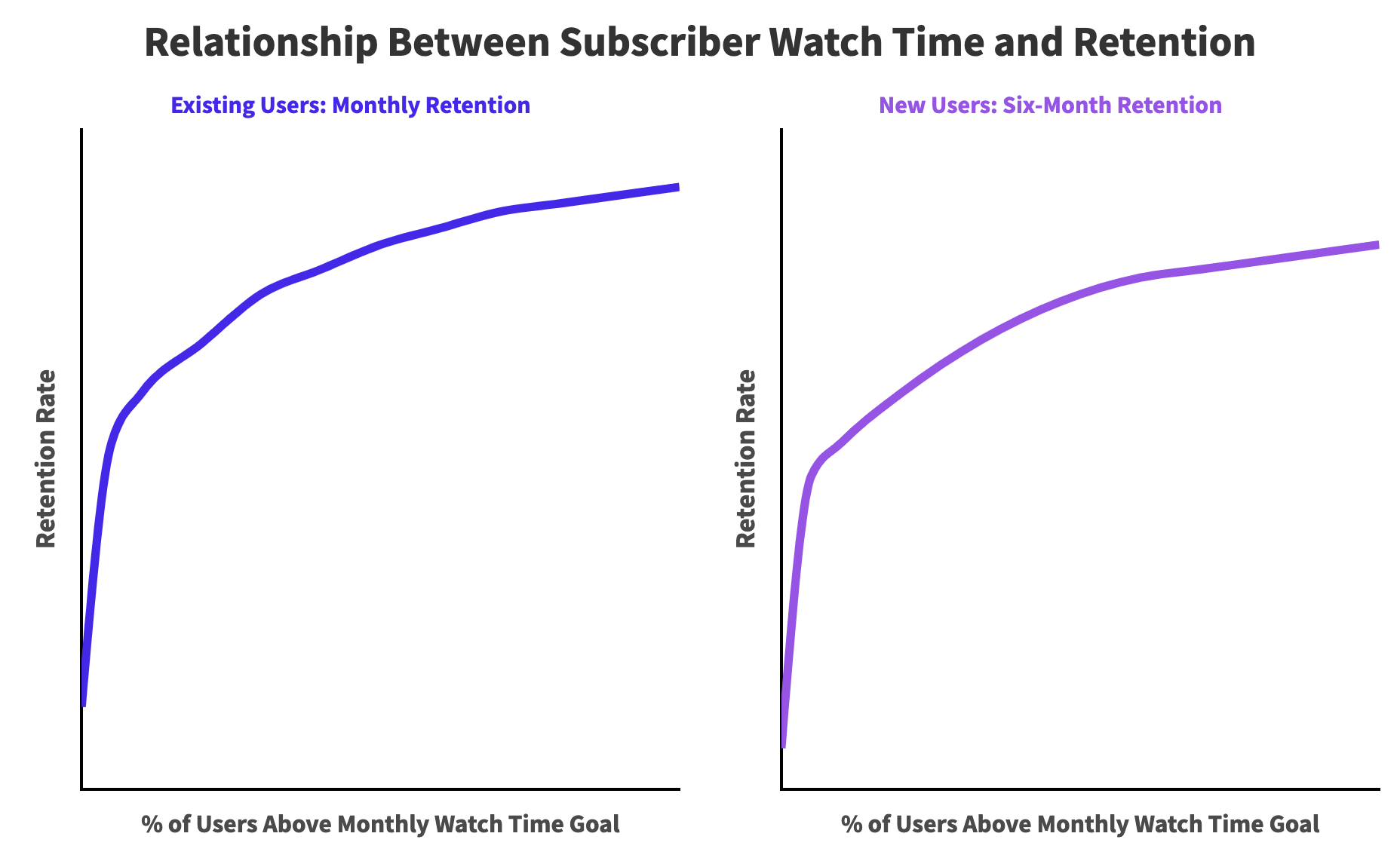
Daniel Parris – The Broken Economics of Streaming Services: A Stats Explainer
https://www.statsignificant.com/p/the-broken-economics-of-streaming
This report examines the financial instability in the streaming industry, focusing on the unsustainable economic models of platforms such as Paramount Plus.
Content Costs and Subscriber Retention
- Expenditure on Content: Streaming services invest heavily in content creation and acquisition to attract subscribers.
- Diminishing Returns: The escalating costs lead to diminishing returns as subscriber growth plateaus.
Competitive Landscape
- Continuous Production: High competition forces continuous, expensive content production to retain subscribers.
Future Projections
- Cable TV Model: The industry may shift towards models resembling traditional cable TV, incorporating advertising, subscription bundling, and higher prices to achieve financial sustainability.
NEWS TV NEWS
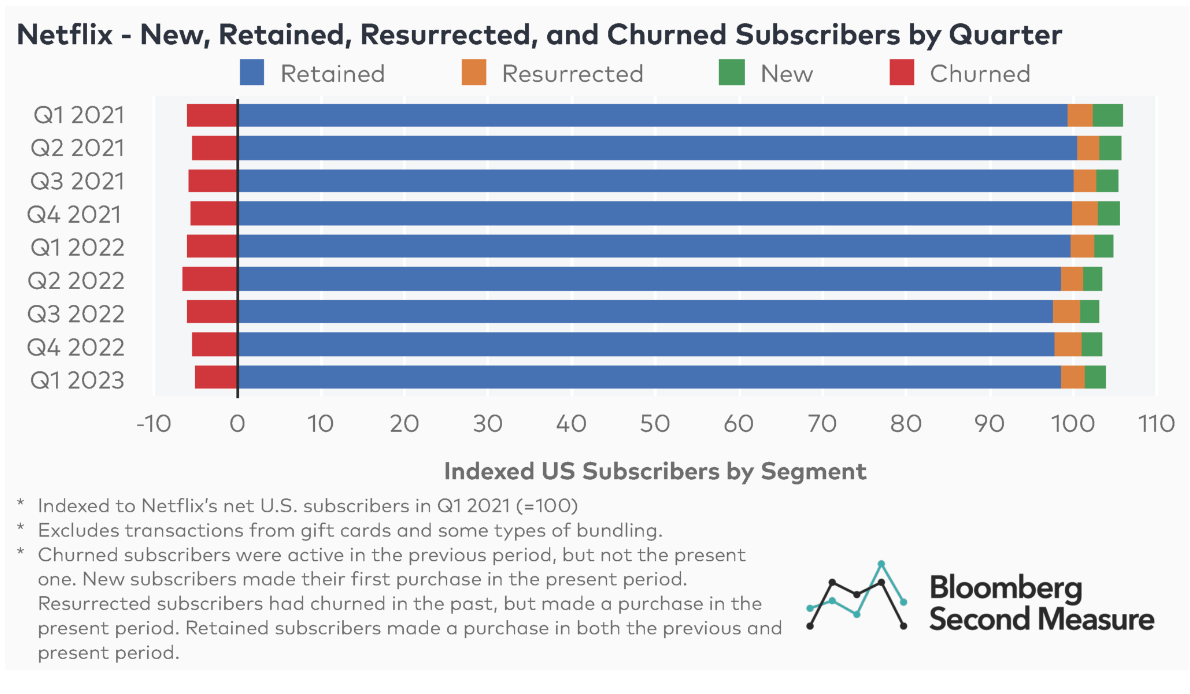
Hollywood’s Top TV Execs Are Happy About The Death Of Peak TV – Here’s Whyhttps://www.slashfilm.com/1593571/peak-tv-dead-hollywood-top-tv-execs-happy/
- Streaming services weren’t required to reveal their subscription numbers or actual viewership
- Shows just needed to look good on paper for investors and stockholders.
- Creators and actors soon learned they weren’t getting paid beyond an initial flat fee; royalties were now gone.
- 600 shows at once wasn’t good for anyone
- Thanks to the strikes, it all came crashing down

FEATURED POSTS
-
Python and TCL: Tips and Tricks for Foundry Nuke
www.andreageremia.it/tutorial_python_tcl.html
https://www.gatimedia.co.uk/list-of-knobs-2

https://learn.foundry.com/nuke/developers/63/ndkdevguide/knobs-and-handles/knobtypes.html
http://www.andreageremia.it/tutorial_python_tcl.html
http://thoughtvfx.blogspot.com/2012/12/nuke-tcl-tips.html
Check final image quality
https://www.compositingpro.com/tech-check-compositing-shot-in-nuke/Local copy:
http://pixelsham.com/wp-content/uploads/2023/03/compositing_pro_tech_check_nuke_script.nkNuke tcl procedures
https://www.gatimedia.co.uk/nuke-tcl-proceduresKnobs
https://learn.foundry.com/nuke/developers/63/ndkdevguide/knobs-and-handles/knobtypes.html
(more…)
-
The Public Domain Is Working Again — No Thanks To Disney
www.cartoonbrew.com/law/the-public-domain-is-working-again-no-thanks-to-disney-169658.html
The law protects new works from unauthorized copying while allowing artists free rein on older works.
The Copyright Act of 1909 used to govern copyrights. Under that law, a creator had a copyright on his creation for 28 years from “publication,” which could then be renewed for another 28 years. Thus, after 56 years, a work would enter the public domain.
However, the Congress passed the Copyright Act of 1976, extending copyright protection for works made for hire to 75 years from publication.
Then again, in 1998, Congress passed the Sonny Bono Copyright Term Extension Act (derided as the “Mickey Mouse Protection Act” by some observers due to the Walt Disney Company’s intensive lobbying efforts), which added another twenty years to the term of copyright.
it is because Snow White was in the public domain that it was chosen to be Disney’s first animated feature.
Ironically, much of Disney’s legislative lobbying over the last several decades has been focused on preventing this same opportunity to other artists and filmmakers.The battle in the coming years will be to prevent further extensions to copyright law that benefit corporations at the expense of creators and society as a whole.




